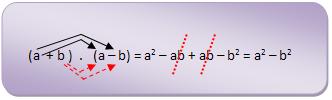Frações algébricas

Fração algébrica é o quociente de divisão de duas expressões algébricas.

Exemplos

a) x/5y
b) (x+y) / (a – 1)
c) ( x – 1) / ( y + 2 )

Observações

1) Nas rações algébricas o numerador e o denominador são polinômios ou monômios
2) O denominador de uma fração nunca pode ser zero
3) As propriedades das frações algébricas são as mesmas das frações aritmética.

SIMPLIFICAÇÃO de frações algébricas

Para simplificar uma fração, basta dividir o numerador e o denominador por seus divisores comuns.

Exemplos

1)15x² / 30x³z =

Passo 1:fatorar os termos da fração
(3⦁5⦁x⦁y⦁y ) / (2⦁3⦁5⦁x⦁x⦁x⦁z )=

Passo 2:cancelar os termos semelhantes
5y² /10x²z

2) ( a² - 9) / ( a + 3) =
[(a + 3) / (a – 3) ] / (a + 3) =
= a – 3

Observe que neste último exemplo, fatoramos os termos da fração e cancelamos os termos comuns.
Uma fração que não admite mais simplificação é chamada de irredutível.

 ADIÇÃO E SUBTRAÇÃO DE FRAÇÕES ALGÉBRICAS

Para adicionar ou subtrair frações algébricas utilizamos as mesmas regras das frações numéricas

a) Frações que apresentam o mesmo denominador.

Somamos ou subtraímos os numerados e conservamos o denominador comum

Exemplo

1) 5x/m + 3x/m = (5x + 3x)/m = 8x/m
2) 7x/6y – 3x/6y = (7x – 3x)/6y = 4x/6y = 2x/3y

b) Frações que apresentam denominadores diferentes.

Devemos reduzir as frações ao mesmo denominador comum e em seguida procedemos como no caso anterior

Exemplo 1

Calcular: (3y / 2x) + (5y / 4x)

Temos m.m.c (2x,4x) = 4x

Logo:
(3y / 2x) + (5y / 4x) =
( 6y/4x) +(5y/4x) =
(6y + 5y) / 4x =
11y/4x

Exemplo 2

Calcular: (5/2x )– (3/4x²)

Temos m.m.c. : (2x,4x²) = 4x²

Logo: 5/2x – 3/4x² =
10x/4x² - 3/4x² =
(10x -3)/4x²

MULTIPLICAÇÃO DE FRAÇÕES ALGÉBRICAS
Para multiplicar frações algébricas procedemos do seguinte modo:
-multiplicamos os numeradores entre si
- multiplicamos os denominadores entres si

Exemplos

Calcular os produtos

1) a/b . x/y = ax/by
2) 3a / x . 7/5y = 21a /5xy
3) 2x/5c . 4x² /3c = 8x³/15c²
4) (x + y)/ 4b . (x – y)/ m = (x² - y²) / 4

Nos casos em que o numerador e o denominador têm fatores comuns, podemos cancelá-los antes de efetuar a multiplicação.

DIVISÃO DE FRAÇÕES ALGÉBRICAS


Multiplicamos a primeira fração pela inversa da segunda.
Exemplos:

Calcular o quociente:

1) 2x/a : 3m/5c = 2x/a . 5c/3m = 10cx/3am
2) 5x²/ 3a : 7b/2x = 5x²/3a . 2x/7b = 10x³/21ab
3) a/ (x+y) : m/(x + y) = a/ (x+y) . (x +y)/m = a/m

POTENCIAÇÃO DE FRAÇÕES ALGÉBRICAS


Elevamos o numerador e o denominador à potência indicada.
Exemplos:
Vamos calcular as potências:
1) (3x²/5am³)² = (3x²)² / (5am³)² = 9x⁴/25a²m⁶
2) (4a/x-3)² = (4a)²/(x-3)² = 16a²/x²-6x+9

                                                                                                                                                                                                                            

 

 

 

Fatoração

Fatoração é escrever um número em forma de um produto de dois ou mais números.Expressões algébricas também podem ser fatoradas.Como por exemplo:

X²+9=(x+3)(x+3)

36-b²=(6+b)(6-b)

X²+4xy+y²=(x+2y)²

Fator comum em        evidência

Podemos usar esse processo só quando temos um fator comum em cada termo da expressão a ser fatorada.Observe a explicação abaixo:

Ex¹:ky+y=

Passo 1:Primeiro devemos observar se em todos os termos da expressão tem um fator em comum(que na situação acima é o y).

Passo 2:Depois colocamos o fator comum em evidência.Assim:

Ex¹:ky+y=y(

Passo 3:Após colocar o termo comum em evidência iremos dividir o termo comum pelos outros termos da expressão , e o resultado será colocado dentro das parênteses.

Ex¹:ky+y=y(k+1)

 

Resultado: A forma fatorada pelo fator comum em evidêcia de ky+y é y(k+1)

Fatoração por agrupamento

Apenas podemos usar este outro processo quando tivermos grupos  de termos com fatores comuns na expressão a ser fatorada.Veja o exemplo:

4a+4b+ax+bx=

Passo1:Primeiro observamos se os termos estão agrupados com fatores comuns.

Passo 2:Colocamos o fator comum de cada grupo evidência.

4a+4b+ax+bx=

4(a+b)x(a+b)=

Passo 3:Colocamos o polinômio comum em evidência.

 4a+4b+ax+bx=

4(a+b)x(a+b)=

(4+x)(a+b)

Resultado:A fatoração por agrupamento de 4a+4b+ax+bx é (4+x)(a+b).

 

Diferença de dois quadrados

 

A diferença entre dois quadrados (a² – b²) é igual ao produto da soma (a + b) pela diferença (a – b).
Justificativa:

Exemplos:
a² – 9 = a² – 3² = (a + 3) . (a – 3)
4x² – 1 = (2x)² – 1² = (2x + 1) . (2x – 1)
81 – m⁶ = 9² – (m³)² = (9 + m³) . (9 – m³)
(a + 1)² – 36 = (a + 1)² – 6² = [(a + 1) + 6] . [(a + 1) – 6] =
= (a + 7) . (a – 5)
4 – (x – y)² = 2² – (x – y)² = [2 + (x – y)] . [2 – (x – y)] = = (2 + x – y) . (2 – x + y)

 

Trinômio quadrado perfeito      

Ele só poderá ser ultilizado quando a expressão algébrica for um trinômio(um polinômio formado por 3 monômios) e esse trinômio fromar um quadrado perfeito.

 

A área dessa figura pode ser calculada por duas formas diferentes:

1^o forma:Como a fórmula para calcular a área de um quadrado é L² e o lado da figura acima é k+a é só elevarmos k+a ao quadrado,assim:

A=(k+a)²

2^o forma:Se o quadrado foi dividido em 4 retângulos onde cada um tem sua própria área ,a soma da área de todos os retângulos é a área total do quadrado maior ficará assim:

A=K²+ka+kA+a²

Como kA e kA são semelhantes podemos adicioná-los,ficando assim:

A=K²+2ka+a²

O resultado K²+2ka+a² é um trinômio.

As duas áreas encontradas representam a área do mesmo quadrado,sendo assim:

K²+2ka+a²=(k+a)²

CUBO DA SOMA DE DOIS TERMOS

 

Cubo da diferença de dois termos

Cubo da diferença de dois termos

produto da soma pela diferença

Regra básica: Quadrado do primeiro termo menos o quadrado do segundo termo

• Exemplos:
  1. 
  2. 

 

Quadrado da diferença de dois termos

Produtos notáveis
Produto notável são produtos de expressões algébricas utilizados com frequência .Abaixo vemos alguns exemplos de produtos notáveis.

(x+y)²=Quadrado da soma de dois termos

(x-y)²=Quadrado da diferença de dois termos

(x+y)(x-y)=Produto da soma pela diferença

(x+y)³=Cubo da soma de dois termos

(x-y)³=Cubo da diferença de dois termos

Vamos conhecer cada um deles.

Quadrado da soma de dois termos

O quadrado da soma de dois termos é igual a:

Quadrado do 1º + 2 vezes o 1º vezes o 2º + o quadrado do 2º.

Ex:(x+y)²=x²+2•x•y+y²

Observe que :

x²=é o quadrado do primeiro termo

2•x•y=é duas vezes o primeiro termo vezes o segundo termo

y²=é o quadrado do segundo termo

(x+y)²=x²+2•x•y+y²

Resultado final = x²+2xy+y²

 

Multiplicação de polinÔmios

Na multiplicação de um monômio por um polinômio,devemos utilizar a propriedade distributiva,na multiplicando o monômio por todos as termos do polinômio e adicionando a seguir , os resultados. Veja o exemplo abaixo:

⇨6a  • (3a+c)=

Passo 1"Aplicar a propriedade distributiva (multiplicando o monômio por todos os termos do polinômio).

⇨6a • (3a+c)=6a•3a+6a•c=

Passo 2"Resolver normalmente os polinômios.

⇨6a • (3a+c)=6a•3a+6a•c=

                              18a²+ 6ac

 

Resultado final = 18a²+ 6ac

 

Divisão de polinÔmios

Caso 1: Divisão de polinômio por polinômio:

Para dividir um polinômio por um polinômio teremos que armar a continha da divisão:

•Escreva o polinômio na ordem decrescente do grau das variáveis:

• Segundo passo é dividir o termo de maior grau do dividendo pelo divisor e depois multiplique o quociente obtido ,pelo divisor ,após isso você irá subtrair do dividendo:
• Repita o mesmo processo.
•A conta acaba quando se tem um resto de grau menor que o grau do divisor .
No final a conta estará mais ou menos assim:

Resultado final=0,ou seja, é uma divisão exata
 

Caso 2: Divisão de polinômio por monômio:

Pra dividir um polinômio por um monômio,devemos dividir os termos do polinômio pelo monômio.

Exemplo:

(35x² + 21X⁵):7X=(35x²:7x)+(21x⁵:7x)=

                                           K       $         K   

                                         5x        +        3x⁴

Pois,35 : 7=5 , e 21:7=3

subtração de polinbomios

Subtração de   polinômios

Vamos considerar os polinômios abaixo:

6ab-7a+8b   e   2b-3a+ab

Resolução:

 6ab-7a+8b – (2b-3a+ab) =

1º passo⇨Fazer o jogo de sinais

6ab-7a+8b – (2b-3a+ab) =

6ab-7a+8b-2b+3a-ab =

2º passo⇨Organizar o polinômio.

6ab-7a+8b – (2b-3a+ab) =

6ab-7a+8b-2b+3a-ab =

6ab-ab-7a+3a+8b-2b =

3º passo⇨Resolver normalmente.

6ab-7a+8b – (2b-3a+ab) =

6ab-7a+8b-2b+3a-ab =

6ab-ab-7a+3a+8b-2b =

     5ab    -4a     +6b

Resultado final⇨5ab-4a+6b

adição de polinomios

Adição de polinômios

Considere os polinômios abaixo:

5a + 3x – ab     e     +7ab - 9x + 8a

Resolução:

5a+3x-ab+7ab-9x+8a =

Primeiro organizamos o polinômio

5a+8a+3x-9x-ab+7ab =

Depois , resolvemos normalmente.

5a+8a+3x-9x-ab+7ab =

   13a    -6x    +6ab

Resultado final⇨13a-6x+6ab

polinomio reduzido em termo semelhante

polinÔmio reduzido em termos semelhante Consideramos o polinômio:

8a+5b-b+5a-3a+5b =

1º passo⇨Organizar o polinômio.   

8a+5b-b+5a-3a+5b =

8a+5a-3a+5b-b+6b =

2º passo⇨Resolver normalmente.

8a+5b-b+5a-3a+5b =

8a+5a-3a+5b-b+5b =

    13a-3a+4b+5b =

       10a   +    9b

Resultado final =10a+9b.

Obs:Podemos somar ou subtrair apenas os termos de mesma variável.

grau de um polinomio

Grau de um polinÔmio

Podemos saber o grau de um polinômio não-nulo determinando o termo de maior grau não-nulo.

Exemplos:

X⁵y⁵+ X³p⁴-x⁵g⁸ é do 13º grau.                                                  

 X⁵y⁵ = 10º grau (pois, 5 + 5 = 10)

X³p⁴ = 7º grau (pois, 3 + 4 = 7)

-x⁵g⁸ = 13º grau (pois, 5 + 8 = 13)

polinomio

polinÔmio

Polinômio(‘’poli’’-grego-muitos) é qualquer adição algébrica de monômios.São exemplos de polinômios:

4x+9y                  3d+9h               55f+64L

 (todos os exemplos acima são binômios , ou seja , um polinômio de dois termos)

Obs:Um polinômio cujo os coeficientes sejam todos iguais a zero , é denominado polinômio nulo .Como por exemplo:

0x     0x²     0y⁶    0p⁴     0d⁵    0h⁷       0t⁸

raiz quadrada de um polinomio

Raiz Quadrada de um           monÔmio  

Obtemos a raiz quadrada de um monômio extraindo a raiz do coeficiente numérico e dividindo por 2 os expoentes das variáveis.Vamos observar o exemplo abaixo:

√4a⁶z⁴ = 2a³z²

Lembrando que,para resolver a equação acima , tiramos a raiz quadrada de 4(que é 2), repetimos as variáveis (que é A e Z ) e dividimos os expoentes das variáveis por 2 e assim obtivemos o resultado , que é 2a³z².              

potenciação de manomios

Potenciação de               monÔmios 

Para sabermos o resultado da potência de um monômio,devemos elevar o coeficiente numérico e a parte literal á potência indicada.Observe o exemplo abaixo:

(3z³)³ =

Em um caso como esse, devemos multiplicar os dois expoentes(o que está dentro dos parênteses e o que está fora também).Veja como vai ficar:

(3z³)³ = 3z^{3 x 3} = 3z⁹

^{Veja este outro exemplo:}

(5a³b²)² =

Neste caso a conta é um pouco mais complicada,mas é o mesmo processo.Vamos ver como fica.

(5a³b²)² = (5)² x (a³) x (b²)²  = 25a⁶b⁴

Divisão de polinomios

Divisão de monômios

 Observe o exemplo abaixo:

(34x⁵) : (2x³)=

Para obtermos o quociente da divisão acima , teremos que dividir os coeficientes numéricos e as Partes literais entre si.A conta ficará assim:

(34x⁵) : (2x³) = (34:2) x  (x⁵:x³) = 17x²

OBS:Lembrando que divisão de potências de mesma base ,  repete a base e subtrai os expoentes